Table of Contents
Functions are essentially mathematical formulas. They are used to store expressions with variable values, arguments. To execute a function, the values for a number of arguments need to specified. These arguments are then inserted into the expression, making it possible to calculate.
Functions are normally entered in an expression by writing the name followed by arguments, separated by commas (or semicolons in languages with comma as decimal point), in parenthesis, thus following the syntax name(arg1, arg2, ...). Qalculate! will give a helpful error message if the arguments are not correct.
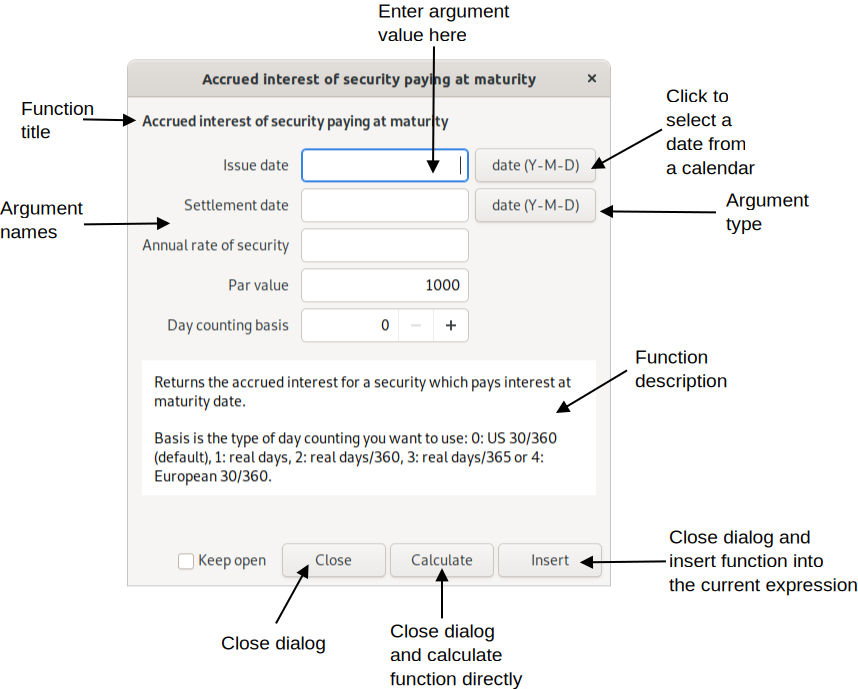
The insert function dialog presents an easy way to insert a function and its arguments.
Although it can lower the readability of an expression, it is perfectly legal to skip the parenthesis and put the arguments after a space, and end with a space or operator. This is most useful in short expressions with single argument functions (e.g. “sqrt 5”).
Argument types include:
Free — anything
Number — a numeric value
Integer — a whole number
Symbol — a defined or undefined unknown variable
Text — a free text string
Date — a date in local or standard format (Year-Month-Day, recommended)
Vector
Matrix
Boolean — 0 for false, 1 for true
Object — the name of a variable, function or unit
Variable — the name of a variable
Function — the name of a function
Unit — the name of a unit
File — the path to a file
Angle — an angle used in trigonometric functions, meaning a number and an angle unit. If no angle unit is included the default is used.
The argument can be restricted by further conditions. For example that a number must be positive.
Most arguments (primarily number arguments) can be replaced by a vector. The function will then be calculated for each vector element and a new vector will be returned. If more than one argument are supplied to a function that takes exactly one argument, each argument will be treated as elements of a vector.
Here the main function categories and some of their members are described, to give an overview of available functions. For information about separate functions and a complete list of all available functions see Appendix A, Function List or the function manager.
- Algebra
Contains sum() and product(), which corresponds to the sum and product signs. solve() solves equations (e.g. “solve(x × 2 = 8)” returns “4” meaning that x equals 4). Use solve2() and multisolve() to solve multiple equations with multiple variables.
- Calculus
Includes diff(), which calculates the derivative of an expression with optional arguments “with respect to” (default x) and “order” (default 1), and a limited integration function.
- Combinatorics
Contains functions such as perm() for permutations, comb() for combinations, and factorial().
- Complex Numbers
Contains functions useful for calculations with complex numbers, including arg() for principal argument and conj() for conjugate.
- Data Sets
A data set consists of a set of properties and objects, which can be accessed by a function which takes two arguments — object and property. The function returns the object's value for the selected property. For example, the data in the “Elements” data set is accessed with the atom() function, with the element (referenced using atomic symbol, number or name) and property (e.g. weight) as arguments. The special property “info” displays all properties of the object in a dialog window.
- Date & Time
Includes days() and yearfrac() which returns the number of days and fractional years, respectively, between two dates.
- Exponents & Logarithms
Standard logarithmic and exponential functions. ln() calculates the natural logarithm of a number, while log() allows a choice of base as the second argument. The cbrt() and root() functions only calculates real roots. For roots of odd degree the root functions give a different answer than the exponential operator, “^”, for negative values (“cbrt(-8) = -(8)^(1/3) = -2”, but “(-8)^(1/3) = 1 + 1.73i”).
- Economics
This essentially includes most of the financial functions that are usually found in spreadsheet applications.
- Elements
This category includes functions to retrieve data such as atomic weight. The atom() function opens a window with available data of an element. These functions accept the number, symbol or name of the element as argument. The data are loaded on demand.
- Geometry
Category with formulas mostly for calculation of circumference, area and volume of geometric shapes.
- Logical
Some procedural functions mainly for use in other functions. These include if(), which tests a conditional expression and returns a value depending on if the expression evaluates true or false, and for(), which processes a value while a condition is true.
- Matrices & Vectors
These are functions that generate, access and process matrices and vectors. The vector() function generates a vector from a variable number of arguments for elements, while matrix() first needs the number of rows and columns and then the elements from left to right. Matrices can also be imported directly from a CSV file with load().
Separate elements at a specified row and column are accessed with element(). Other functions include det() for calculation of the determinant of a matrix and inverse() which returns the inverse of the given matrix, as well as functions such as sort() and rank().
- Miscellaneous
A category for functions that do not fit elsewhere.
- Number Theory
Contains subcategories arithmetic, number bases, and rounding, in addition to functions such as abs(), which returns the absolute value of a number (“|” can also be used; e.g. “|-5| = abs(-5) = 5”, and gcd(), the greatest common divisor. round() is the standard rounding function. The functions for number bases translates a text string, representing an expression with numbers in a different base, to a decimal number. Includes bin() for binary numbers, hex() for hexadecimal numbers, oct() for octal numbers and base() for numbers in a any other base.
- Special Functions
Includes beta(), gamma() and similar functions, as well as Riemann zeta (zeta()) and Kronecker delta (kronecker()).
- Statistics
Contains a lot of functions for descriptive statistics and some statistical tests. Data sets are stored as vectors. Generally, functions with a vector/data set as last argument can take elements/samples as a variable number of arguments directly instead of in a vector (e.g. “mean(1, 2, 3)” equals “mean(vector(1, 2, 3))”). Also contains the rand() function, which returns a pseudo random number between 0 and 1 (with no argument, or zero), or a random integer between one and the specified number.
- Trigonometry
Trigonometric functions, including sin(), cos(), tan(), sec(), csc(), cot(), and hyperbolic and inverse versions of those. These functions take as argument an angle. If the default angle unit ( → ) is set to none, the argument must have an angle unit appended (degrees, radians or gradians), otherwise the default unit will be appended automatically (and removed from result of inverse functions).
- Utilities
Various utility functions. Most are only useful in definition of other functions. The save() function can however be a quick way of storing a value in a variable, and csum() can be a powerful tool for data processing. This category also contains some functions, such as char() and ascii(), that might be useful for programmers. replace() provides an easy way of replacing unknown variables by known expressions in a value (e.g. “replace(5x^2 + x, x, 3)” equals “5 × 3^2 + 3”).
Functions are a bit more complex than variables, but can nevertheless be relatively easily created. Select → → , or click the on the keypad or in the function manager and a function edit dialog pops up.
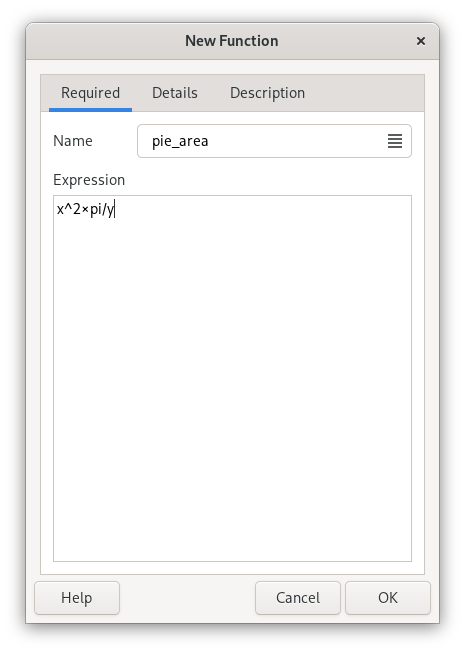
The function edit dialog is divided in three pages, where the first page contains the only required properties — name and an expression. x, y and z with or without (default) a backslash are used as argument placeholders in the expression.
First enter a name, used to reference the function in an expression. Then enter an expression below.
The expression of a function is basically a normal expression with placeholders for arguments. The expression “x^4” creates a function which calculates the fourth power of a single argument. If you name it for example “sqsq”, “sqsq(2)” will calculate “2^4”.
The argument placeholders consist of a backslash and a letter — x, y, z for the 1st, 2nd and 3rd arguments and a to u for argument 4 to 24. The backslash can however be omitted, but avoids any possible conflict with existing variables, units and functions used in the expression. The argument symbols are replaced by entered arguments when a function is calculated. They also decide the number of arguments that a function requires. For example the function for triangle area (“base × height / 2”) has the name triangle and the expression “(\x × \y)/2”, which gives that “triangle(2, 3)” equals “(2 × 3) / 2” and returns “3” as result. An argument can be used more than one time and all arguments must not necessarily be in order in the expression.
Additionally, optional arguments can be put in the expression with upper-case (X, Y, Z, ...) instead of lower-case letters (x, y, z, ...). The default value should be put in curly brackets after the letter (e.g. “\X{2}”). The default value may be omitted and is then zero. All additional arguments after an optional argument must also be optional.
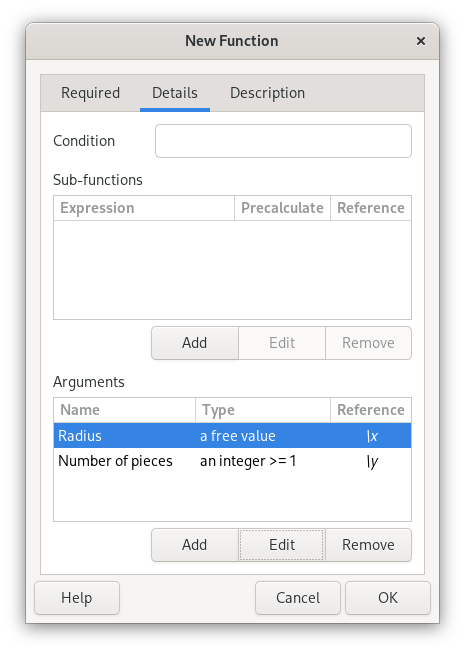
A required condition, sub-functions, and argument definitions can optionally be specified in the second page (“Details”).
The condition specifies an expression which must evaluate true before the function is calculated. This follows the same conventions as function expressions. For example, if the value of the second argument must be higher than the first, “\y > \x” may be entered as a condition.
Sub-functions can be useful for complex functions, they use the same syntax as the main expression, and are references using a backslash followed by a number (e.g. “\1” for the first sub-function). The sub-function can be inserted in the main expression as a precalculated value or intact (meaning that the subfunction might be recalculated for each occurrence in the main expression).
Name, type, and required conditions can be specified for each argument.
The third page allows entering of category, descriptive name (shown as title in menus) and description. The function can also be hidden from menus with the corresponding check box, which can be useful for functions only used in other functions.
Global, system-wide functions can not actually be changed by the user, but if one of these functions is edited, they are deactivated and seemingly replaced by a new function. Some functions are however hard-coded and cannot be changed by the user. Once the user function is removed or deactivated the original function is automatically reactivated.